Understanding the Derivative of x^x in Differential Calculus
Written on
Chapter 1: Introduction to Derivatives
In this section, we delve into the concept of derivatives, specifically focusing on the function x^x.
To understand this, we will utilize the natural logarithm on both sides of the equation.
Section 1.1: Applying the Natural Logarithm
Using the natural logarithm allows us to simplify the expression effectively.
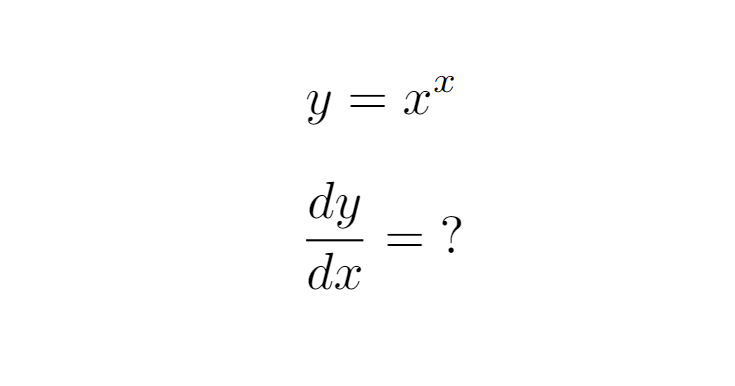
Next, we proceed with implicit differentiation.
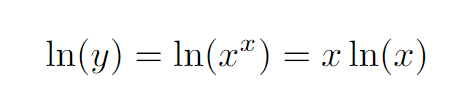
We then apply the product rule for differentiation.
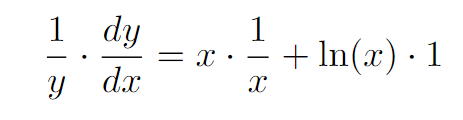
After rearranging, we find the derivative dy/dx.

Remember that y represents our original function, leading us to our final result.
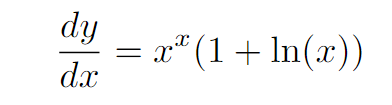
Section 1.2: Using the Exponential Function
Another effective method for finding the derivative involves leveraging properties of the exponential function and the natural logarithm.
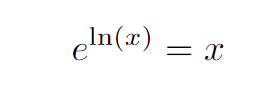
Consider how this manipulation can aid in our differentiation process.

To differentiate, we apply the chain rule.
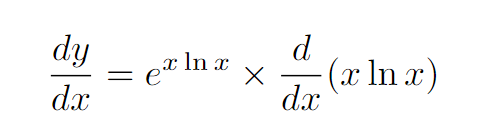
We again utilize the product rule in our calculations.
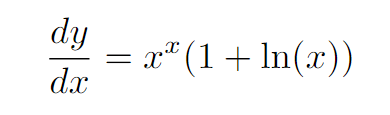
It’s noteworthy that the expression e^(xlnx) simplifies directly to x^x, providing us with the sought-after answer.
And that concludes our exploration. Isn't it fascinating?
What were your thoughts during this process? Share your insights in the comments; I’m eager to hear from you!
This video explains the derivative of x^x step by step, helping to visualize the concepts discussed.
This second video further elaborates on the derivative of x^x, offering additional examples and explanations.
Chapter 2: Conclusion and Resources
Don't forget to explore more intriguing math puzzles available on Medium, covering a range of topics from algebra to number theory. Share this with your friends!
If you enjoyed this content, consider signing up for updates whenever I publish new articles. Thank you for your support!
